Question

A bus travels at an average speed of 60 miles per hour on the highway. Once inside city limits, the bus decreases its speed by 55%

Answer 1

27 mph

Explanation:

im doing the iready quiz too

Answer 2

Thus the speed of the bus after it decreased by 55% is now 27 miles per hour.

Explanation:

In this solution and based on the information given we assume that the question is:

"What is the speed of the bus after it decreased by 55%?"

We know the original value of the speed is
`60(m)/(h)`

We know that the speed decreased by
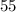`55`% of it's original value, where
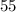`55`% is the equivalent of
`(55)/(100)=0.55`

To find the new value (lets call it
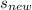`s_(new)`) we have to find the 55% of the original value and then subtract it from the original as follow:

`s_(new)=60-60(0.55)\\s_(new)=60-33\\s_(new)=27(m)/(h)`

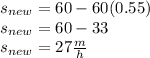
Thus the speed of the bus after it decreased by 55% is now 27 miles per hour.