Answer:
x = 5.3 units
Explanation:
The given triangle has adjacent sides as 6 and 9 units. It has an angle bisector, which divides the angle between the adjacent sides, and opposite side in lengths x and 8 units.
An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle.
This means,
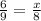
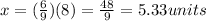
Thus, the value of x is 5.3 units.