Question

`4m {}^(2)= 3`
​

Answer 1

`m=-(\sqrt3)/(2)\ and\ m=(\sqrt3)/(2)`

Explanation:

Given:

The equation given to solve is:

`4m^2=3`

First, we divide both sides by 4. This gives,

`(4m^2)/(4)=(3)/(4)\\\\m^2=(3)/(4)`

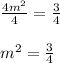
Now, we take square root on both sides. This gives,

`√(m^2)=\pm\sqrt{(3)/(4)}`

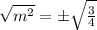
We know that from the definition of square root function that:

`√(x^2)=x`

`\sqrt{(x)/(y)}=(√(x))/(√(y))`

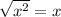
Therefore,

`√(m^2)=m`

`\sqrt{(3)/(4)}=(√(3))/(√(4))=(\sqrt3)/(2)`

`m=\pm(\sqrt3)/(2)`

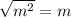
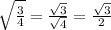
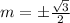
Hence, two values of 'm' are possible. They are:

`m=-(\sqrt3)/(2)\ and\ m=(\sqrt3)/(2)`