Question

12. Three kinds of tickets were sold for a concert. Main floor tickets cost $35, balcony tickets cost $25 and

gallery tickets cost $15. The box office sold 475 tickets for a total of $13,275. There were 45 more floor
tickets sold than balcony tickets.
Write a system of three equations to find how many tickets of each kind were sold, Interpret your answer to
show how many tickets of each kind were sold.

Answer 1

Hence the system of three equations to find the tickets sold are given below;

`x= y+45`

`x+y+z = 475`

`35x+25y+15z=13275`

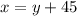
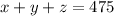
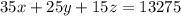
Also Number of each tickets sold are,

Number of Main floor ticket sold = 220

Number of balcony tickets sold = 175.

Number of gallery ticket sold = 80.

Explanation:

Let Number of Main floor ticket sold be x.

Let number of balcony tickets sold be y.

Let the number of gallery ticket sold be z.

Given:

Total tickets sold = 475

Also There were 45 more floor tickets sold than balcony tickets.

Hence we can say that;

`x= y+45 \ \ \ \ \ \ equation \ 1`

Now Total tickets sold is the sum of Number of Main floor ticket sold and number of balcony tickets sold and the number of gallery ticket sold be z.

Hence we can say that the equation is;

`x+y+z = 475 \ \ \ \ equation\ 2`

Now Substituting the value of equation 1 in equation 2 we get;

`x+y+z=475\\y+45+y+z=475\\2y+z= 430 \ \ \ \ equation\ 3`

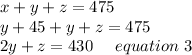
Also Given:

Cost of main floor ticket = $35

Cost of balcony ticket = $25

Cost of gallery ticket = $15

Total Money made = $13,275

Now we know that Total Money made is equal to sum of Cost of main floor ticket multiplied with Number of main floor ticket and Cost of balcony ticket multiplied by Number of balcony tickets and Cost of gallery tickets multiplied with number of gallery ticket.

Computing the above statement in equation form we get;

`35x+25y+15z=13275 \ \ \ \ equation\ 4`

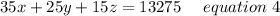
Hence the system of three equations to find the tickets sold are given below;

`x= y+45`

`x+y+z = 475`

`35x+25y+15z=13275`

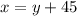
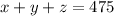
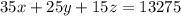
Now Substituting the value of equation 1 in equation 4 we get;

`35(y+45)+25y+15z=13275\\35y+1575+25y+15z = 13275\\60y+15z = 13275-1575\\60y+15z=11700`

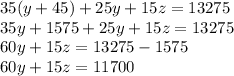
Now Dividing by 15 on both side we get;

`(60y)/(15)+(15z)/(15)=(11700)/(15)\\\\4y+z=780 \ \ \ \ equation\ 5`

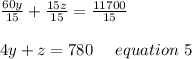
Now Subtracting equation 3 from equation 5 we get;

`(4y+z)-(2y+z)=780- 430\\\\4y+z-2y-z= 350\\\\2y=350\\\\y=(350)/(2)=175`

Now Substituting the value of y in equation 1 we get;

`x=y+45\\x=175+45\\x=220`

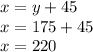
Now Substituting the value of x and y in equation 2 we get;

`x+y+z=475\\220+175+z=475\\395+z=475\\z=475-395\\z=80`

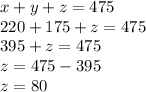
Hence;

Number of Main floor ticket sold = 220

Number of balcony tickets sold = 175.

Number of gallery ticket sold = 80.