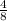Question

In a certain fraction, the numerator is 4 less than the denominator. If 4 is added to both the numerator and the denominator , the resulting fraction is equal Vhat was the original 8/12 fraction (not necessarily written in lowest terms

Answer 1

The original fraction was
`(4)/(8)`

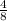
Explanation:

The correct question is

In a certain fraction, the numerator is 4 less than the denominator. If 4 is added to both the numerator and the denominator , the resulting fraction is equal to 8/12. What was the original fraction (not necessarily written in lowest terms)

Let

x ----> the numerator of the original fraction

y ----> the denominator of the original fraction

`(x)/(y)`

we know that

`x=y-4`

so

the original fraction is

`(y-4)/(y)`

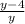
If 4 is added to both the numerator and the denominator , the resulting fraction is equal to 8/12

so

`(y-4+4)/(y+4)=(8)/(12)`

`(y)/(y+4)=(8)/(12)`

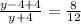
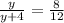
Solve for y

`12y=8y+32\\12y-8y=32\\4y=32\\y=8`

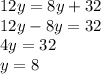
Find the value of x

`x=y-4`

`x=8-4=4`

therefore

The original fraction was

`(4)/(8)`