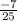Question

Given tan theta=4/3 and pi

Answer 1

76.57295824...

Explanation:

1. tan Ø =4/3pi

2.( tan^-1)tan Ø =4/3pi(tan^-1)

-Multiply by 2nd tan or tan to the negative first power on both sides

3. Answer = 76.8 (rounded to the nearest tenths)

Answer 2

cos 2Ф =
`(-7)/(25)`

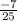
Explanation:

From the question above, we are ask to find cos 2Ф

To solve this problem, we need to first know what formula to use.

Using multiple formula;

cos 2Ф = cos²Ф - sin²Ф

since tan Ф is given as 4/3, then we need to first find sin Ф and cos Ф

tan Ф =
`(4)/(3)` =
`(opp)/(adj)`

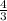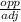
from the above, opposite = 4 adjacent =3

hypotenuse = ?

we need to find the hypotenuse

Let hyp = x

using Pythagoras theorem,

hyp² = opp² + adj²

= 4² + 3²

=16 + 9

= 25

hyp = √25

hyp = 5

opposite = 4 adjacent = 3 hypotenuse= 5

sinФ =
`(opposite)/(hypotenuse)` =
`(4)/(5)`

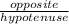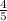
cos Ф =
`(adjacent)/(hypotenus)` =
`(3)/(5)`

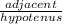cos 2Ф = cos²Ф - sin²Ф

=
`((3)/(5) )^(2)` -
`((4)/(5)) ^(2)`

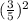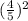
cos 2Ф =
`(9)/(25)` -
`(16)/(25)`

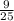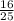
cos 2Ф =
`(-7)/(25)`