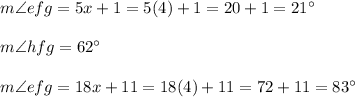Question

What is m<efh =(5×+1)°,m<hfg =62° and m <efg = (18×+11)°, find each measure.​

Answer 1

x = 4

m<EFH = 21

m<EFG = 83

Explanation:

First you must put the angles into an equation then solve as you would in Algebra:

5x + 1 + 62 = 18x + 11

5x - 18x + 1 + 62 = 11

m-13x + 63 = 11

-63 -63

-13x = -52

-13 -13

x = 4

Then plug in the 4

5(4) + 1

20 + 1

21

m<EFH = 21

18(4) + 11

72 + 11

83

m<EFG = 83

Answer 2

`m\angle efg=21\°\\\\m\angle hfg=62\°\\\\m\angle efg=83\°`

Explanation:

Given:

`m\angle efh=5x+1\\m\angle hfg=62\\m\angle efg=18x+11`

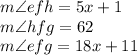
Now, from the figure shown below,

The sum of angle efh and angle hfg is equal to the angle efg. This is true because of the angle addition postulate which states that when two angles are formed with the same vertex and different sides, then their sum is equal to the total angle made by both the sides at the vertex.

Here, point 'f' is the vertex and the sides are 'ef and 'fg'.

Therefore,

`m\angle efh+m\angle hfg=m\angle efg`

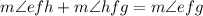
Plug in their values and solve for 'x'. This gives,

`5x+1+62=18x+11\\5x+63=18x+11\\18x-5x=63-11\\13x=52\\x=(52)/(13)=4`

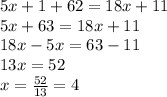
Therefore, the angle measure of each are:

`m\angle efg=5x+1=5(4)+1=20+1=21\°\\\\m\angle hfg=62\°\\\\m\angle efg=18x+11=18(4)+11=72+11=83\°`