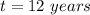Question

Suppose that a new employee starts working at $7.17 per hour and receives a 3% raise each year. After time t, in years, his hourly wage is given by the equation y=$7.17(1.03)^to. Find the amount of time after which he wi l be earning $10.00 per hour. After what amount of time will the employee be earning $10.00 per hour?

Answer 1

12 years

Explanation:

Exponential Growing

Some variables tend to grow in time following an exponential function. The general equation for y as a function of t is

`y=b.r^(at)`

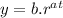
The case given in the question corresponds to the following function

`\displaystyle y=7.17(1.03)^t`

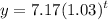
We want to know the amount of time after which the function will be 10, or

`\displaystyle 7.17(1.03)^t=10`

Rearranging

`\displaystyle 1.03^t=(10)/(7.17)`

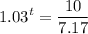
Solving for t

`\displaystyle Ln1.03^t=Ln((10)/(7.17))`

`\displaystyle t.Ln1.03=Ln((10)/(7.17))`

`\displaystyle t=(Ln((10)/(7.17)))/(Ln\ 1.03)`

`\displaystyle (0,3327)/(0,02959)`

`\displaystyle t=11.26\ years`

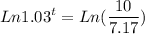
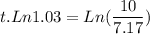
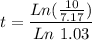
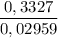
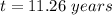
When t=11 years, the employee is not paid at $10 per hour yet. We must jump to the next integer value.

`t=12\ years`