Question

A small garden measures 9 ft by 13 ft. A uniform border around the garden increases the total area to 192 ft square. What is the width of the border ​

Answer 1

The width of border is 1.5 feet

Solution:

Given that small garden measures 9 ft by 13 ft

A uniform border around the garden increases the total area to 192 ft square

To find: width of border

Let the width of border be "x"

Then the new measures of garden are (9 + 2x) feet and (13 + 2x) feet

The total area of garden = 192 square feet

`(9 + 2x)(13 + 2x) =192`

`117 + 18x + 26x + 4x^2 = 192\\\\4x^2 + 44x - 75 = 0`

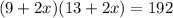
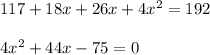
Let us solve the above equation by quadratic formula

`\text {For a quadratic equation } a x^(2)+b x+c=0, \text { where } a \\eq 0\\\\x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

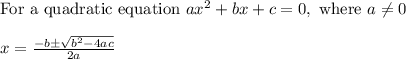
Using the above formula,

For
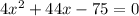`4x^2 + 44x - 75 = 0` , we have a = 4 ; b = 44 ; c = -75

Substituting the values of a = 4 ; b = 44 ; c = -75 in above quadratic formula we get,

`\begin{aligned}&x=\frac{-44 \pm \sqrt{44^(2)-4(4)(-75)}}{2 * 4}\\\\&x=(-44 \pm √(1936-1200))/(8)\\\\&x=(-44 \pm √(3136))/(8)\\\\&x=(-44 \pm 56)/(8)\end{aligned}`

`\begin{aligned}&x=(-44+56)/(8) \text { or } x=(-44-56)/(8)\\\\&x=(12)/(8) \text { or } x=(-100)/(8)\\\\&x=1.5 \text { or } x=-12.5\end{aligned}`

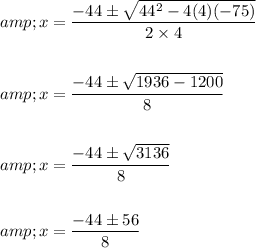
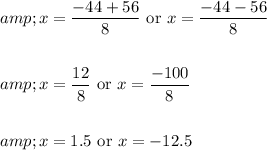
Since "x" cannot be negative,

we get x = 1.5

Thus width of border is 1.5 feet