Question

determine the diameter to the nearest inch of a large can of tuna that has a volume 6068 inches and a height of 3.3 inches

Answer 1

The diameter of can is 48 inches.

Explanation:

Given:

Volume of can = 6068 inches.

And height(h) = 3.3 inches.

Now, to find the diameter.

Diameter = 2 × radius

Let radius be
`r.`

So, by putting the formula of volume we get the radius:

`Volume =\pi r^2h`

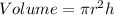
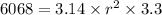`6068=3.14* r^2* 3.3` (taking the value of π=3.14)

`6068=10.362* r^2`

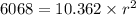
Dividing both sides by 10.362 we get:

`585.60=r^2`

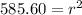
Using square root on both sides we get:

`24.199=r`

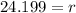
Radius = 24.199 inches.

Then, we get the diameter:

Diameter = 2 × radius

Diameter = 2 × 24.199 = 48.398 inches.

Diameter = 48 inches (rounding to nearest, inch as in the place of tenth it is 3 which is less than 5.)

Therefore, the diameter of can is 48 inches.