Question

Which table shows a proportional relationship between X and Y?

X. 2,4,5,6
Y. 6,12,18,21

X. 3,5,7,8
Y. 1.5, 2.5, 3, 4.5

X. 1,3,4,5
Y. 50,150,200,250

X. 1,2,3,6
Y 1.5,3,6,9

Answer 1

table 3

explanation: I got this question in time4learning and got it right

Answer 2

Table 3

X. 1,3,4,5

Y. 50,150,200,250

Explanation:

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
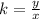`k=(y)/(x)` or
`y=kx`

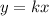
Verify each table

Find the value of k for each ordered pair

If the value of k is the same for all ordered pairs, then the table represents a proportional relationship.

If the k-value is different for any of the ordered pairs, then the table does not represent a proportional relationship

Table 1

For x=2, y=6 --->
`k=(y)/(x)` ---->
`k=(6)/(2)=3`

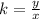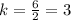
For x=4, y=12 --->
`k=(y)/(x)` ---->
`k=(12)/(4)=3`

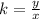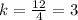
For x=5, y=18 --->
`k=(y)/(x)` ---->
`k=(18)/(5)=3.6`

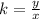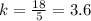
The values of k are different

therefore

The table 1 not represent a proportional relationship

Table 2

For x=3, y=1.5 --->
`k=(y)/(x)` ---->
`k=(1.5)/(3)=0.5`

For x=5, y=2.5 --->
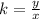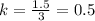
`k=(y)/(x)` ---->
`k=(2.5)/(5)=0.5`

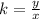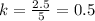
For x=7, y=3 --->
`k=(y)/(x)` ---->
`k=(3)/(7)=0.4`

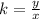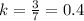
The values of k are different

therefore

The table 2 not represent a proportional relationship

Table 3

For x=1, y=50 --->
`k=(y)/(x)` ---->
`k=(50)/(1)=50`

For x=3, y=150 --->
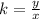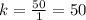
`k=(y)/(x)` ---->
`k=(150)/(3)=50`

For x=4, y=200 --->
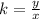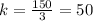
`k=(y)/(x)` ---->
`k=(200)/(4)=50`

For x=5, y=250 --->
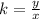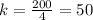
`k=(y)/(x)` ---->
`k=(250)/(5)=50`

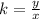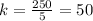
The values of k are the same

therefore

The table 3 represent a proportional relationship

Table 4

For x=1, y=1.5 --->
`k=(y)/(x)` ---->
`k=(1.5)/(1)=1.5`

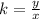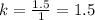
For x=2, y=3 --->
`k=(y)/(x)` ---->
`k=(3)/(2)=1.5`

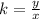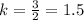
For x=3, y=6 --->
`k=(y)/(x)` ---->
`k=(6)/(3)=2`

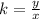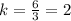
The values of k are different

therefore

The table 4 not represent a proportional relationship