Question

A pendulum 2m long is released from rest when string makes 30 degree with the vertical.find speed of 70g bob and the tension

Answer 1

The velocity = 5.82[m/s], Tension = 1.78 [N]

Step-by-step explanation:

We can solve this problem using the principle of energy conservation and Newton's second law.

Here we can find an attached image of the pendulum with a free body diagram, where we can see the forces acting over the pendulum.

The initial data are:

`m_(ball) = 70 [g] o 0.07[gr]`

The pendulum is released when the string is at 90° with respect to the vertical axis. Therefore the initial velocity is zero = 0, and the initial kinetic energy will be zero also.

The expression that defines the kinetic energy and the work is the following equation.

`E_(k1) + W_(1-2) = E_(k2)\\where:\\E_(k1) =kinetic energy at point 1. E_(k1) =0\\W_(1-2)= work \\E_(k2) = kinetic energy at point 2.\\0 + W_(1-2) = E_(k2)\\`

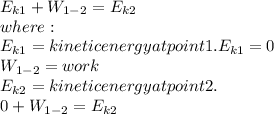
We take the reference point where the pendulum is matching the vertical axis. At this point the potential energy is zero and all the potential energy has been transformed into kinetic energy.

Now analyzing once again the expression deducted, we have:

`(m*g*h)-(m*g*(2-1.73))=(1)/(2) *m*v_(2) ^(2) \\(0.07*9.81*2)-(0.07*9.81*(2-1.73))=(1)/(2) *(0.07)*v_(2) ^(2)\\1.188=(1)/(2) *(0.07)*v_(2) ^(2)\\\\v_(2)=\sqrt{(1.188*2)/(0.07) }\\ v_(2)= 5.82[m/s]`

In the free body diagram, we can see the forces and the equation to find the tension T. Especial attention must be seen to notice that the acceleration to find the tension in the equation should be the normal acceleration.

The normal acceleration is defined by:

`a_(n) =(v_(2)^(2)  )/(L)`

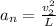
Clearing the tension T, this value is 1.78 [N]