Question

Can anybody help me that smarter than me

Answer 1

Question 5: y = 6.69 ft

Question 6: z = 12.52 in

Explanation:

Question 5

In the right triangle shown, with respect to the angle given, y is the side that is "opposite" and the known side (15) is the "hypotenuse".

Note: The side opposite of right angle is the hypotenuse

Which trigonometric ratio relates "opposite" and "hypotenuse"? It is "SINE".

Let's setup the ratio and solve for y:

`Sin(26.5)=(y)/(15)\\y=15*Sin(26.5)\\y=6.69`

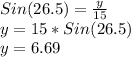
So,

y = 6.69 feet

Question 6

With relation to the angle given, we have the "adjacent" side and the "hypotenuse".

Which trigonometric ratio relates "adjacent" with "hypotenuse"?

It is COSINE!

We can set up a ratio as the previous question and solve for z:

`Cos(37)=(10)/(z)\\z=(10)/(Cos(37))\\z=12.52`

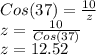
So,

z = 12.52 inches