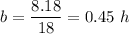Answer:
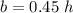
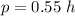
Explanation:
Cinematics
When an object moves at a constant speed, it can be computed as

Where x is the distance traveled and t the time needed to complete it at the constant speed v
If we wanted to compute t from the equation above, then
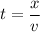
Elia rode her bicycle from her house to the beach at 18 km/h and then from the beach to the park at 15 km/h, taking 1 hour in the whole travel, each distance being equal. If we call b as the number of hours it took Elia to ride from her house to the beach, and p the number of hours it took her to ride from the beach to the park, then we can compute
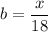

The question doesn't ask for something in particular, so I'm helping you by solving the complete problem. We know the total time is 1 hour, so
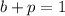
Replacing b and p
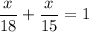
Multiplying by 90
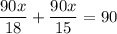
Simplifying and solving for x
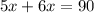
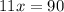
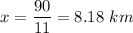
We finally compute b and p