Question

Factor the polynomial given that f(k) = 0

x^3 - 5x^2 - 2x + 24; k = -2


I'm hoping somebody can explain how to figure out one of these problems.

Answer 1

The following polynomial can be factorized as,

f(x) =
`(x-4)(x-3)(x+2)`

Explanation:

It is given that at x = -2, the value of polynomial is zero, thus, by factor theorm,

(x+2) is the factor of the above polynomial.

By dividing the given polynomial by (x+2), we get,

F(x) =
`(x-4)(x^(2) -7x +12)`

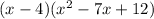
This can be further simplified as,

`(x^(2) -7x +12)` =
`(x^(2) -4x-3x+12)`

=
`(x(x-4)-3(x-4))`=
`(x-3)(x-4)`

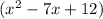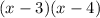
Thus the polynomial becomes,

f(x) =
`(x-4)(x-3)(x+2)`