Question

An inline skater skates on a circular track 120.0 m in diameter at a tangential speed of 9.20 m/s. If the skater’s mass is 68.5 kg what is the magnitude of the centripetal force on the skater?

Answer 1

The centripetal force acting on the skater is 48.32 N.

Step-by-step explanation:

Given:

Radius of circular track is,
`R=120.0\ m`

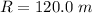
Tangential speed of the skater is,
`v=9.20\ m/s`

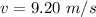
Mass of the skater is,
`m=68.5\ kg`

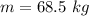
We are asked to find the centripetal force acting on the skater.

We know that, when an object is under circular motion, the force acting on the object is directly proportional to the mass and square of tangential speed and inversely proportional to the radius of the circular path. This force is called centripetal force.

Centripetal force acting on the skater is given as:

`F_c=(mv^2)/(R)`

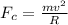
Now, plug in the given values of the known quantities and solve for centripetal force,
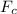`F_c`. This gives,

`F_c=(68.5* (9.20)^2)/(120.0)\\\\F_c=(68.5* 84.64)/(120)\\\\F_c=(5797.84)/(120)\\\\F_c=48.32\ N`

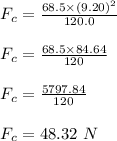
Therefore, the centripetal force acting on the skater is 48.32 N.