Question

Ellen can walk home from school from by either two routes. One takes her along two adjacent sides of a rectangular park whose length is 20 meters more than its width. The other route is a short cut long the diagonal of the rectangle. If the diagonal route is 40 meters shorter than the other route, what are the exact dimensions of the park?

Answer 1

The exact dimensions of the park is 80 meters by 60 meters.

Explanation:

Let the width of the rectangular park is W meters, then its length will be (W + 20) meters.

Now, given that the diagonal route is 40 meters shorter than the other route.

Hence,
`(W + W + 20) - \sqrt{W^(2) + (W + 20)^(2)} = 40`

⇒
`2W - 20 = \sqrt{W^(2) + (W + 20)^(2)}`

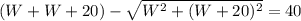
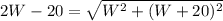
Now, squaring both sides we get,

(2W - 20)² = W² + (W + 20)²

⇒ 4w² - 80W + 400 = 2W² + 40W + 400

⇒ 2W² = 120W

⇒ W = 60 meters

Now, length is (60 + 20) = 80 meters

Therefore, the exact dimensions of the park is 80 meters by 60 meters. (Answer)