Question

What is the solution to the system of equations graphed below?

y=1/2x+ 2
y = -2x - 3
OOO
O A. (0, -3)
O B. (-2,1)
O c. (0, 2)
O D. (-4,0)

Answer 1

Answer: B. (-2,1)

Explanation:

Hi, to answer this question we have to solve the system of equations:

y=1/2x+ 2

y = -2x - 3

Multiplying the first equation by 4 and adding both equations:

4y = 2x +8

+

y = -2x - 3

---------------

5y = 5

y =5/5

y=1

Replacing the value of y in any equation:

y = -2x - 3

1 = -2x - 3

Solving for x:

2x =-3-1

2x=-4

x =-4/2

x =-2

So, the solution is

x =-2; y = 1

The correct option is B. (-2,1)

Answer 2

Option B) (-2,1) is correct.

Explanation:

The given equations are,
`y=1/2x+ 2   and   y = -2x - 3`.

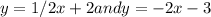Let the point of intersection be (a,b).

Thus (a,b) satisfies both the equations.

`b=1/2a+ 2`

`b = -2a - 3`

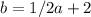
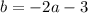
subtracting both the equations we get,

`((5)/(2))(x) = -5`

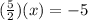
x = -2, now inserting this value in anyone of the equations,

`y = -2(-2) -3 = 4-3 = 1`

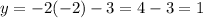
Thus, the intersection point is (-2,1).