Question

Which of the following triangles is not a right triangle?

a) 3 cm, 4 cm, 5 cm
b) 6 ft, 8 ft, 12 ft
c) 27 cm, 36 cm, 45 cm
d) none of the above

Answer 1

Answer: Option b.

Explanation:

Let's check each triangle with the Pythagorean Theorem:

`a^2=b^2+c^2`

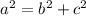
Where "a" is the hypotenuse (the longest side) and "b" and "c" are the legs of the right triangle.

a) Given:

`a=5\ cm\\b=3\ cm\\c=4\ cm`

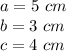
You get:

`(5 cm)^2=(3 cm)^2+(4 cm)^2\\\\25\ cm^2=25\ cm^2`

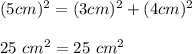
(This is a right triangle)

b) Given:

`a=12\ ft\\b=8\ ft\\c=6\ ft`

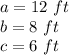
You get:

`(12\ ft)^2=(8\ ft)^2+(6\ ft)^2\\\\144\ ft^2\\eq 100\ ft^2`

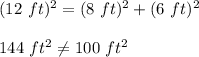
(This is not a right triangle)

c) Given:

`a=45\ cm\\b=36\ cm\\c=27\ cm`

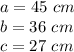
You get:

`(45\ cm)^2=(36\ cm)^2+(27\ cm)^2\\\\2,025\ cm^2=2,025\ cm^2`

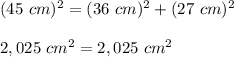
(This is a right triangle)