Question

A certain forest covers an area of 3800 km^2. Suppose that each year this area decreases by 7.25%. What will the area be after 8 years

Answer 1

Area of forest after 8 years
`\boldsymbol\approx` 2081.11
`\mathbf{km^(2)}`

Explanation:

Rate of decrements is 7.25% per year.

Let us create a function 'f(x)' which gives the area of forest left after 'x' years.

f(0) means the initial year when the area is 3800
`\textrm{km}^(2)`.

f(0) = 3800

f(1) means the area left after one year passed when the area decreased by 7.25% than previous year which is 3800
`\textrm{km}^(2)`

f(1) = 3800 - 7.25% of 3800 =
`3800-(7.25)/(100)*3800` =
`3800(1-(7.25)/(100))` =
`3800((92.75)/(100))`

f(2) means the area left after two year passed when the area decreased by 7.25% than previous year which is f(1)

f(2) = f(1) - 7.25% of f(1) =
`\textrm{f}(1)((92.75)/(100))` =
`3800((92.75)/(100))((92.75)/(100))` =
`3800((92.75)/(100))^(2)`

.

.

.

.

.

Similarly
`\mathbf{f(x)=3800((92.75)/(100))^(x)}`

`\textrm{f}(8)=3800((92.75)/(100))^(8)\approx2081.11 \ \textrm{km}^(2)`

`\mathbf{\therefore f(8)\approx2081.11 \ km^(2)}`

Answer 2

The area of forest after 8 years , decreases at the rate of 7.25% is 2081.108 square kilometers .

Explanation:

Given as :

The initial area of forest = 3800 square kilometer

The rate of decrease of area every year = r = 7.25 %

The time period for its decrease = t = 8 years

Let The forest area after 8 years = A square kilometers

Now, According to question

The forest area after 8 years = Initial area of forest ×
`(1-(\textrm rate)/(100))^(\textrm time)`

or, The forest area after 8 years = 3800 km² ×
`(1-(\textrm r)/(100))^(\textrm t)`

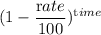
or, The forest area after 8 years = 3800 km² ×
`(1-(\textrm 7.25)/(100))^(\textrm 8)`

Or, The forest area after 8 years = 3800 km² ×
`(0.9275)^(8)`

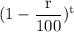
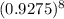
Or, The forest area after 8 years = 3800 km² × 0.54766

Or, The forest area after 8 years = 2081.108 km²

So, Area of forest after 8 years = 2081.108 km²

Hence The area of forest after 8 years , decreases at the rate of 7.25% is 2081.108 square kilometers . Answer