Question

Given: ∆ABC –iso. ∆, m∠BAC = 120°

AH ⊥ BC , HD⊥ AC
AD = a cm, HD = b cm
Find: P∆ADH

Solve without Using Pythagorean Theorem

Answer 1

`P = a + b + \sqrt{a^(2) + b^(2)}`

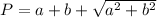
Explanation:

See the attached diagram.

Given that, Δ ADH is a right triangle with ∠ ADH = 90°.

So, applying Pythagoras Theorem

AH² = AD² + DH² = a² + b²

⇒
`AH = \sqrt{a^(2) + b^(2)}` {Neglecting the negative root as AH can not be negative}

Therefore, the perimeter of the triangle Δ ADH = AD + AH + DH

⇒
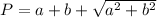`P = a + b + \sqrt{a^(2) + b^(2)}` (Answer)