Answer and Explanation to questions 13,14,15
13)
 as given in the question.
as given in the question.
14)
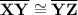 Since Y is the midpoint of XZ. So, Y will divide XZ in equal halves into XY and YZ.
Since Y is the midpoint of XZ. So, Y will divide XZ in equal halves into XY and YZ.
15)
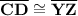
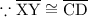 and
and
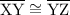 . So,
. So,
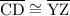
Answer and Explanation to questions 16,17,18
∠3 is supplementary to ∠1 means: ∠3 + ∠1 = 180°
And, according to figure ∠1 + ∠2 = 180° as ∠1 and ∠2 form a straight line.
∠3 + ∠1 = 180° .............(i)
∠1 + ∠2 = 180° .............(ii)
subtracting equation (i) and (ii) will give ∠3 = ∠2 ..........(iii)
15) ∠3 is supplementary to ∠1 as given in the question
16) ∠2 is supplementary to ∠1 as shown be equation (ii)
18) ∠3 ≅ ∠2 as shown by equation (iii)
Answer and Explanation to questions 19
∠3 and ∠4 form a straight line. Therefore, ∠3 + ∠4 = 180° .......(i)
∠4 and ∠5 form a straight line. Therefore, ∠4 + ∠5 = 180° .......(ii)
subtracting equation (i) and (ii)
∠3 + ∠4 - (∠4 + ∠5) = 180°-(180°)
∠3 + ∠4 - ∠4 - ∠5 = 180°-180°
∠3 - ∠5 = 0
∴ ∠3 = ∠5 (Hence Proved)