Question

The ratio of the width to the length of a rectangle is 2:3, respectively. Answer each of the following. b The width is increased by 25%. By what percent should the length change to keep the area the same?

Answer 1

Answer: The length should be reduced by 20%

Explanation:

The ratio of the width to the length of a rectangle is 2:3, respectively , this means that

W =
`(2)/(3)`L

Area of rectangle is given as Length x width , this means

A = L X W

Substituting into the Area , we have

A = L x
`(2)/(3)`L

A =
`(2)/(3)`
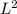`L^(2)` ..................... equation 1

Width is increased by 25 % , so new width = 1.25W

Let the increase in Length be x , then new Length = L + x

Area = Length x Width

A = (L+x) X 1.25W

Recall that W =
`(2)/(3)`L , then

A = (L + x ) X 1.25(
`(2)/(3)`L)

A = (L + x ) X
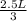`(2.5L)/(3)` ....................................... equation 2

Since we need to keep the Area the same , we will equate the two equations , this means that

`(2)/(3)`
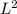`L^(2)` = (L + x ) X
`(2.5L)/(3)`

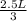
Which implies :

2
`L^(2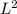)` = 2.5L(L + x )

divide through by 2.5L

0.8L = L + x

Therefore :

x = 0.8L - L

x = - 0.2 L

Since x represents the change in L and it gives negative , this means that the Length should be reduced by 20% to keep the area the same