Answer:
The approximate perimeter of the parallelogram is 20.63 units
(or 21 units if rounded up completely)
Explanation:
In principle we know that the Perimeter of a Parallelogram is given by:
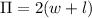 Eqn. (1)
Eqn. (1)
where
 is the Perimeter,
is the Perimeter,
 is the width and
is the width and
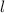 is the length of the parallelogram. We also know that since we have a Parallelogram rectangle it means that the two widths will be of equal size and the two lengths will also be of equal size.
is the length of the parallelogram. We also know that since we have a Parallelogram rectangle it means that the two widths will be of equal size and the two lengths will also be of equal size.
Now lets call each point as:
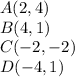 Eqn. (2)
Eqn. (2)
then we have a Parallelogram ABCD where AB and CD can be our widths and BD and DA can be the lengths (or vice versa).
Since we know the vertices, we can compute each side of the parallelogram (i.e. AB, BC, CD and DA) using the distance formula that in principle reads:
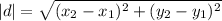 Eqn. (3)
Eqn. (3)
Thus using the values from Eqn. (2) and the formula of Eqn. (3) for each side we have:

Which proves that since
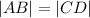 and
and
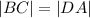 our calculations are correct and ABCD is in fact a parallelogram. So now we have all sides, and recalling Eqn. (1) and plugging in our values (where we can say
our calculations are correct and ABCD is in fact a parallelogram. So now we have all sides, and recalling Eqn. (1) and plugging in our values (where we can say
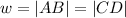 and
and
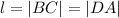 we have:
we have:
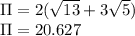 units
units
which can be rounded up as ≅
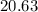 units or ≅
units or ≅
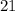 .
.