Answer:
See the verification below.
Explanation:
Starting expression:
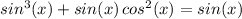
Extract from the expression on the left of the equal sign the common factor "sin(x)":
![sin^3(x)+sin(x)\,cos^2(x)=sin(x)\\sin(x)[sin^2(x)+cos^2(x)]=sin(x)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/nw80x3guu0mp5sfjac4o32e92cu3j3udhz.png)
Now use the Pythagorean trigonometric identity:
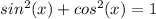 to replace the expression in between square brackets with "1":
to replace the expression in between square brackets with "1":
![sin(x)[sin^2(x)+cos^2(x)]=sin(x)\\sin(x) \,[1]=sin(x)\\sin(x)=sin(x)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/82trhpcci9nkzhv8bp3ueily3ljn9kod8j.png)
Therefore we have verified the identity