Answer: y = 2x + 10
Explanation:
Two lines are said to be parallel if they have the same slope.
The given line is 6x - 3y = 15 , to find the slope of the line , we will make y the subject of the formula , that is
6x - 3y = 15
6x - 15 = 3y
dividing through by 3 , we have
2x - 5 = y
Therefore : y = 2x - 5
comparing with the formula of line in slope - intercept form
y = mx + c
where m is the slope
therefore , the slope is 2
since the new equation of the line is parallel to the one above , that means the slope is also 2.
To find the equation of the line , we will use the formula for calculating equation of line in slope - point form
y -
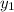= m ( x -
= -4
= 2
m = 2
Substituting into the formula , we have
y - 2 = 2 ( x - {-4} )
y - 2 = 2 ( x + 4 )
y - 2 = 2x + 8
adding 2 to both sides , we have
y = 2x + 10