Question

A town has a population of 8000 in Groves at 4.5% every year to the nearest year how long will it be until the population will reach 22,500

Answer 1

It takes 10 years approximately for the population to reach 22,500

Explanation:

Given:

Initial population = 8000

Population growth rate 4.5 %

Future population = 22500

To Find:

Time taken to reach a population of 22500

Solution:

The population growth can be identified by using

`N = N_0e^((rt))`

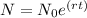
where

N is future popluation

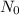`N_0` is the initial population

t is the time taken

r is the rate of the growth

Here we have to find the time t, rephrasing the formula

`log((N)/(N_0)) = rt`

`(log((N)/(N_0)))/(r) = t`

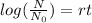
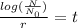
Substituting the values we get,

`t = (log((22,500)/( 8000)))/( 0.045)`

`t = (log(2.8125))/( 0.045)`

`t = ( 0.449)/( 0.045)`

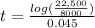
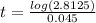
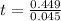
t = 9.97

t=10(approx)