Question

In 2005, John invested $50,000 in the stock market. By 2011 his

investment had grown to $52,200. Find an equation relating time as x and
the value of the investment as y. If the market continues to grow at the
same rate, how much will be in his account in 2016? Explain what the
slope represents for this problem.

Answer 1

3y = 150000 + 1100x ; x as time in years and y as amount of investment after x years.

Step-by-step explanation:

`\textrm{rate at which market is growing}= \frac{\textrm{Growth in the investment}}{\textrm{Number of years passed to grow}}`

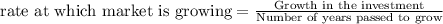
Growth in John's investment between year 2005 and 2011 = $(52200 - 50000) = $2200

Years passed to grow that much = 2011 - 2005 = 6 years

`\textrm{rate}=(2200)/(6)`

`\mathbf{rate=(1100)/(3)}`

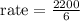
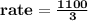
Value of investment after x years = (Initial investment) + (Rate of growth) × (Years of investment)

Value of investment = y

Years of investment = x

rate of growth =
`(1100)/(3)`

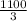
Initial investment = $50000

`\mathbf{y=50000+(1100)/(3)* x}`

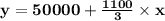
∴ 3y = 150000 + 1100x

slope of above equation of line is
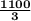`\mathbf{(1100)/(3)}` which the rate of growth of market.