Question

Adratic Formula

11.
Find the number of real number solutions for the equation.
he Quadratic
100%
X2 + 5x + 7 = 0
criminant and
ng Data
0
The Discriminant
deling Data
90%
0
test
xpressions and

Answer 1

Explanation:

discriminant=5²-4×1×7=25-28=-3<0

no real number solution.

Answer 2

There are no real solutions for the equation
`x^(2)+5x+7`.

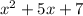Explanation:

For a quadratic equation given by
`ax^(2)+bx+c=0`

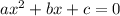
The number of real solutions are determined by discriminant D.

D=
`b^(2)-4ac`

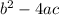
if D>0 then the roots are real and distinct

if D=0 then roots are real and equal

if D<0 then real roots do not exist.

In this case,

a=1 b=5 and c=7

`D=b^(2)-4ac=5^(2)-4*1*7=-3 < 0`

Since D<0, there are no real solutions.