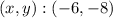Question

Solve using the addition method. -5x-y=38, -6x-3y=60

Answer 1

For this case we have the following system of equations:

`-5x-y = 38\\-6x-3y = 60`

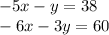
To solve the system we follow the steps below:

We multiply by -3 the first equation:

`15x + 3y = -114`

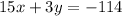
We have the following equivalent system:

`15x+3y=-114\\-6x-3y=60`

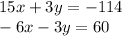
We add the equations:

`9x = -54\\x = - \frac {54}{9}\\x = -6`

We look for the value of the variable "y":

`-5x-y = 38\\-5 (-6) -y = 38\\30-y = 38\\-y = 38-30\\-y = 8\\y = -8`

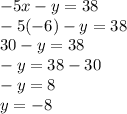
The system solution is given by:

`(x, y): (- 6, -8)`

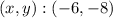
Answer:

`(x, y): (- 6, -8)`