Answer:
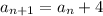
Explanation:
Have in mind the definition of the term
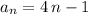 , and now work on what the term
, and now work on what the term
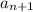 is based on the previous definition:
is based on the previous definition:
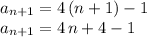
In the next step do NOT combine the numerical values, but try to identify the
 term (
term (
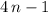 ) in the expression (notice the use of square brackets to group the relevant terms):
) in the expression (notice the use of square brackets to group the relevant terms):
![a_(n+1)=4\,n+4-1\\a_(n+1)=[4\,n-1]+4\\a_(n+1)=a_n+4](https://img.qammunity.org/2020/formulas/mathematics/middle-school/on2g0wuav9xbll0fi9i9pujnqihletq893.png)
So now we have the term "
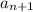 " defined in a recursive manner based on the previous term "
" defined in a recursive manner based on the previous term "
 "
"