Question

URGENT!!! 50 POINTS!!! Consider the polynomial functions P (x) and Q (x)​ , where neither polynomial is a constant function.

Determine whether each of the following related functions below will be polynomial function. fill in the blank with Always, Sometimes, or Never for each related function.

P(x) + Q(x)​

P(x) · Q(x)​

P(x) / Q(x)​​

1 / P(x)​​

Answer 1

Always

Always

Sometimes

Never

Explanation:

P(X) + Q(X)

Sum of two polynomials is always a polynomial.

For example, Let P(x) = 3x² and Q(x) = 5x

P(x) + Q(x) = 3x² + 5x

This is again a polynomial.

In other words, we can say that Polynomial is closed under addition.

P(x) . Q(x)

Product of two polynomials is again a polynomial.

Let P(x) = 2x and Q(x) = a constant function, 5

Then the product = 10x, is again a polynomial.

Multiplication of two polynomials is closed.

P(x) / Q(x)

This need not always be a polynomial. When Q(x) = a constant function zero, i.e., Q(x) = 0, then the function is not defined.

But let's say P(x) = 5x² and Q(x) = x.

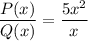`$ (P(x))/(Q(x)) = (5x^2)/(x) $` = 5x, a polynomial.

So, is a polynomial sometimes.

We can, say Division is not always closed.

1/Q(x)

This could never be a polynomial. This is not even in the form of a polynomial. So,
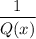`$ (1)/(Q(x) )$` is never a polynomial.

Hence, the answer.