Question

If a student randomly guesses at 20 multiple-choice questions, find the probability that the student gets exactly four correct. Each question has four possible choices.

Answer 1

Probability = 0.190

Explanation:

Given:

Number of questions, 'n' = 20

Each question has four choices.

Let event of choosing correct answer be success and its probability be represented by 'p'.

Therefore, event of choosing wrong answer is failure and its probability be represented by 'q'.

Now, probability of success is choosing one correct answer out of 4 options. So,
`p=(1)/(4)=0.25`

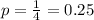
Now, 'p' and 'q' are complements of each other. Therefore,

`q=1-p=1-0.25=0.75`

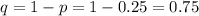
Now, we need 4 successes. Therefore,
`x=4`

Using Bernoulli's theorem to find 'x' successes from 'n' questions, we get:

`P(x)=_(x)^(n)\textrm{C}p^xq^(n-x)`

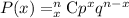
Plug in 4 for 'x', 20 for 'n', 0.25 for 'p' and 0.75 for 'q'. Solve.

`P(4)=_(4)^(20)\textrm{C}(0.25)^4(0.75)^(20-4)\\P(4)=_(4)^(20)\textrm{C}(0.25)^4(0.75)^(16)\\P(4)=4845* (0.25)^4* (0.65)^(16)\\\\P(4)=0.1896\approx0.190`

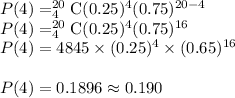
Therefore, the probability of getting 4 correct answers out of 20 questions is 0.190.