Question

Dana is on a train traveling at a speed of 20 km/h. Dana walks from the front of the train to the back of the train at a speed of 4 km/h. What is Dana's speed relative to the ground?

Answer 1

Diana's speed relative to ground is 16 km/h in the direction of motion of train.

Step-by-step explanation:

Given:

Velocity of train in forward direction is,
`v_(t,g)=20\ km/h`

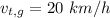
Here,
`v_(t,g)\to \textrm{velocity of the train relative to ground.}`

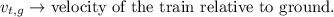
Velocity of Diana relative to train in the backward direction is,
`v_(D,t)=-4\ km/h`

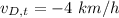
Negative sign implies backward motion or motion opposite to the direction of train's motion. Here, Diana is walking from front of train to back. So, Diana is moving in the opposite direction.

Now, we know that, for two bodies 'A' and 'B', velocity of 'A' relative to ground is given as:

`v_(A,g)=v_(B,g)+v_(A,B)`

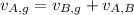
Therefore, velocity of Diana relative to ground is given as:

`v_(D,g)=v_(t,g)+v_(D,t)`

`v_(D,g)=(20-4)\ km/h`

`v_(D,g)=16\ km/h`

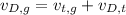
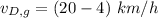
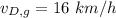
So, Diana's speed relative to ground is 16 km/h in the direction of motion of train.