Question

Can someone help me understand and do this because well I have no idea what I’m doing.

Answer 1

Read Below!

Explanation:

Answer:

Explanation:

Please find attached an edited image of yours where I have named the sides of triangle in part 23). Below I shall give you a detail answer for part 23) along with the final values for the other parts 24) and 25) and you can apply the same methods to solve the remaining two.

So lets consider Triangle 23):

Here we have a Triangle of sides a, c and (b+43) which is the base (total length). We also have line h which is the height of our triangle. Here the height creates a right angle (i.e. 90° ) denoted by the little square symbol in the bottom of the line. This h line divides our triangle into Two Right Triangles. Right triangles mean that one of their angles is ALWAYS 90° .

In theory we also know that the SUM of the interior angles of ANY triangle is always 180°. Finally we know that for ANY Right Triangle the Pythagorian Theorem is true which denotes that the Squared value of the Hypotenuse of the triangle is equal to the squared values of the other two legs of the triangle, which in mathematical form reads:

`x^2+y^2=h^2`

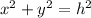
where
`x` and
`y` are the two legs of a right triangle and
`h` is the hypotenuse. In a right triangle we also know that for any of the other two angles (i.e. NOT the 90° angle), thus lets call one of the two remaining angles
`\theta` the following trigonometric identities are to be true:

`sin\theta=(opposite side)/(hypotenuse) \\cos\theta=(adjacent side)/(hypotenuse)\\tan\theta=(opposite side)/(adjacent side)`

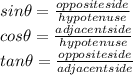
Finally we know that the Area of any triangle is given as half the product of the height (h) and base (b) of the triangle as follow:

`A=(1)/(2)bh`

-----------------------------------------------------------------------------------------------------------

Let us now consider my attached image and the triangle in 23). With respect to the angles, we know 2 out of the 3 angles since one is given as 70° and the other is the right angle, thus 90°. So lets call the uknown one as
`\theta` so we have:

`70+90+\theta=180\\\theta=180-160\\\theta=20`

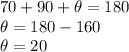
So now we have a Right triangle where we know all 3 angles and 1 of each sides. Therefore we can find the remainder of the sides using our Trigonometric Identities and Pythagorian Theorem on the left right triangle (i.e. a-h-43). Note here
`a` is the hypotenuse,
`h` and
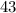`43` are the opposite and adjacent sides, respectively.

Solving for side
`a` we have:

`cos70=(43)/(a) \\a=(43)/(cos70) \\a=125.7\\a=126`

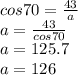
Thus from Pythagoras Theorem:

`a^2 = h^2 + 43^2\\h^2=a^2-43^2\\h=√(a^2-43^2)\\h=√(126^2-43^2)\\h=118`

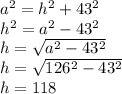
Now let as work on the other right triangle included in our main triangle of 23) as follow. Here now we know
`h` which is the opposite side from the known angle of 37° (that is given), so by trigonometry on the right angle now we have:

`sin37=(h)/(c)\\c=(h)/(sin37)\\ c=196`

So now we can also find the value for side
`b` by Pythagorean theorem as:

`c^2=h^2+b^2\\b^2=c^2-h^2\\b=√(c^2-h^2)\\b=√(196^2-118^2)\\ b=156`

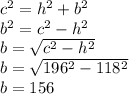
So finally to find the Area of Triangle 23) we know that

Base:
`43+b = 43+156 = 199`

Height:
`h=118`

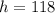
Thus Area formula gives us that:

`A=(1)/(2)(height)(base)\\ A=(0.5)(118)(199)\\A=11741`

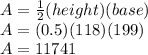
To summarise:

Triangle 23):

Height: 118

Base: 43 + 156 = 199

Area: 11741

Triangle 24):

Height: 11

Base: 5 + 13 = 18

Area: 99

Triangle 25):

Height: 38

Base: 22 + 34 = 56

Area: 1064

Note: ALL values are rounded up to nearest tenth as mentioned in your question