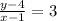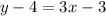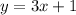Question

What is the equation of the tangent line to the function y=2x - x + 3 at x= 1

a. y=4x+8
b. y=4x-8
c. y=4x-6
d. y=4x

Answer 1

Question:

What is the equation of the tangent line to the function y=2x^2 - x + 3 at x= 1

a. y=4x+8

b. y=4x-8

c. y=4x-6

d. y=4x

Answer:

The equation of tangent is y = 3 x+1

Explanation:

Given the equation of the tangent line to the function
`y=2 x^(2)-x+3`

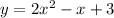
Need to find out the equation of tangent at x = 1

We know that the equation of tangent for any function at point A is

`(y-y_(1))/(x-x_(1))=\text {slope of line at point } A`

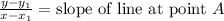
According to question,
`x_(1)=1`

To find out the value of
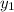`y_(1)`, we put the value of
`x_(1)` in the given equation as,

`y_(1)=2\left(x_(1)\right)^(2)-\left(x_(1)\right)+3=2 *(1)^(2)-1+3=4`

Slope of line at x=1 is

`\text {slope}=4 x_(1)-1=4 * 1-1=3`

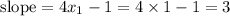
So the required equation of tangent is

`(y-4)/(x-1)=3`

`y-4=3 x-3`

`y=3 x+1`