Answer:
Mrs. Salinas buys 4 ounces M&Ms and 6 ounces Peanuts.
Explanation:
Given,
Total weight of the mixture = 10 pounds.
Total money Mrs. Salinas paid = $24.
We have to find out the weight of each M&Ms and peanuts.
Solution,
Let the weight of M&Ms be x.
And the weight of peanuts be y.
Since total weight of the mixture is 10 pounds.
So, we can frame it in equation as;

Again, Total money paid by Mrs. Salinas is the sum of weight of M&Ms multiplied by price for each ounce and weight of peanuts multiplied by price for each ounce.
So, we can frame it in equation as;
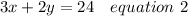
Now, multiplying equation 1 by 2, we get;
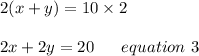
Now subtract equation 3 from equation 2, we get;
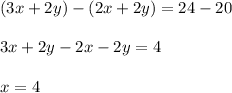
On substituting the value of x in equation 1, we get;

Hence Mrs. Salinas buys 4 ounces M&Ms and 6 ounces Peanuts.