Question

Solve this problem out

Answer 1

The equation D has (1-i) as a solution

Explanation:

we know that

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

Option A

in this problem we have

`x^(2) +2x-2=0`

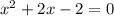
so

`a=1\\b=2\\c=-2`

substitute in the formula

`x=\frac{-2(+/-)\sqrt{2^(2)-4(1)(-2)}} {2(1)}`

`x=\frac{-2(+/-)√(12)} {2}`

`x=\frac{-2(+/-)2√(3)} {2}`

`x=-1(+/-)√(3)`

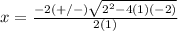
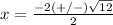
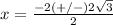
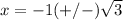
Has two real solutions

Option B

in this problem we have

`x^(2) +2x+2=0`

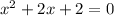
so

`a=1\\b=2\\c=2`

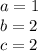
substitute in the formula

`x=\frac{-2(+/-)\sqrt{2^(2)-4(1)(2)}} {2(1)}`

`x=\frac{-2(+/-)√(-4)} {2}`

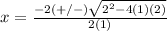
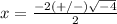
Remember that

`i=√(-1)`

`x=\frac{-2(+/-)2i} {2}`

`x=-1(+/-)i`

`x=-1+i`

`x=-1-i`

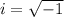
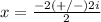
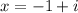
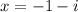
Option C

in this problem we have

`x^(2) -2x-2=0`

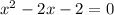
so

`a=1\\b=-2\\c=-2`

substitute in the formula

`x=\frac{-(-2)(+/-)\sqrt{-2^(2)-4(1)(-2)}} {2(1)}`

`x=\frac{2(+/-)√(12)} {2}`

`x=\frac{2(+/-)2√(3)} {2}`

`x=1(+/-)√(3)`

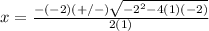
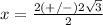
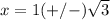
Has two real solutions

Option D

in this problem we have

`x^(2) -2x+2=0`

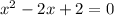
so

`a=1\\b=-2\\c=2`

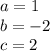
substitute in the formula

`x=\frac{-(-2)(+/-)\sqrt{-2^(2)-4(1)(2)}} {2(1)}`

`x=\frac{2(+/-)√(-4)} {2}`

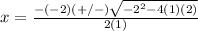
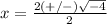
Remember that

`i=√(-1)`

`x=\frac{2(+/-)2i} {2}`

`x=1(+/-)i`

`x=1+i`

`x=1-i`

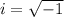
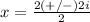
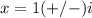
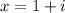
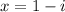
therefore

The equation D has (1-i) as a solution