The function uses W as the variable but the options show only x's as the variable, so I'm asumming W in the answer
Answer:
0 < W < 50
Correct option: A
Explanation:
Domain of functions
Some functions have restricted values of the independent variable x. It can be due to mathematical restrictions, like dividing by 0 or taking the square root of a negative number, of it can be due to practical conditions of the situation being modeled.
In this case, the area of a rectangle is given by the quadratic function.
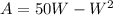
Since the area of a rectangle cannot be negative (and should be positive, though it could be zero), the practical domain of A is determined when
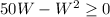
Taking common factor W
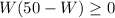
Since W must be positive W>0
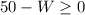
Or equivalently
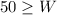

The total interval is
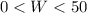
Correct option: A
Please note: The real restriction should be

if we allowed the area to be positive, but I'm providing the most possible correct available option