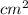Question

The diameter of the larger circle is 12.5 cm. The diameter of the smaller circle is 8.5 cm.

What is the best approximation for the area of the shaded region?

Answer 1

Question:

The diameter of the larger circle is 12.5 cm. The diameter of the smaller circle is 3.5 cm.

What is the best approximation for the area of the shaded region?

Use 3.14 to approximate pi.

Small circle inside big circle, shaded region outside smaller circle and inside larger circle.

Answer:

The area of the shaded region is 65.94
`cm^2`

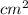
Explanation:

Given:

Diameter of the small circle = 8.5 cm

Diameter of the Large circle = 12.5 cm

To Find:

The area of the shaded region(refer the below diagram)

Solution:

Step 1 : Finding the area of the small circle

Area of the circle =
`\pi r^2`

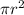
where

r is the radius

we have only diameter

so radius =
`(diameter)/(2)`

=>
`(8.5)/(2)`

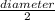
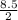
=>4.25

Now

Area of small circle

=>
`\pi * (4.25)^2`

=>
`\pi * (4.25) * (4.25)`

=>
`\pi * 18.06`

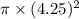
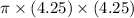
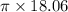
=>56.71
`cm^2`

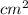
Step 2 : Finding the area of the large circle

Radius =
`(diameter)/(2)`

=>
`(12.5)/(2)`

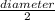
=>6.25

Area of large circle

=>
`\pi * (6.25)^2`

=>
`\pi * (6.25) * (6.25)`

=>
`\pi * 39.06`

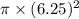
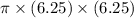
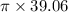
=>122.65
`cm^2`

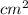
Step 3 : Finding the area of the shaded region

The area of the shaded region = Area of large circle - Area of small circle

The area of the shaded region = 122.65 - 56.71

The area of the shaded region = 65.94
`cm^2`