Answer:
The best approximation for the area of the shaded region is
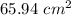
Explanation:
The complete question is
The diameter of the larger circle is 12.5 cm. The diameter of the smaller circle is 8.5 cm.
What is the best approximation for the area of the shaded region?
Use 3.14 to approximate pi.
Small circle inside big circle, shaded region outside smaller circle and inside larger circle
we know that
To find out the area of the shaded region subtract the area of the smaller circle from the area of the larger circle
Remember that
The area of the circle is
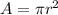
so
![A=\pi [r_1^(2)-r_2^(2)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/lwyeg5x602sx1nyk456xcs1ufuf19do3qu.png)
where
r_1 is the radius of the larger circle
r_2 is the area of the smaller circle
we have
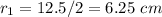 ---> the radius is half the diameter
---> the radius is half the diameter
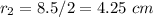 ---> the radius is half the diameter
---> the radius is half the diameter
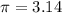
substitute
![A=3.14[6.25^(2)-4.25^(2)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ozah6sj266jq65a8gr16ggppbyvxhf3dzz.png)
