Answer:
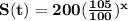
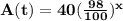
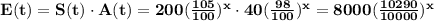
Explanation:
The predicted number of students over time, S(t)
Rate of increment is 5% per year.
A function 'S(t)' which gives the number of students in school after 't' years.
S(0) means the initial year when the number of students is 200.
S(0) = 200
S(1) means the number of students in school after one year when the number increased by 5% than previous year which is 200.
S(1) = 200 + 5% of 200 =
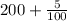 =
=
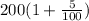 =
=
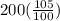
S(2) means the number of students in school after two year when the number increased by 5% than previous year which is S(1)
S(2) = S(1) + 5% of S(1) =
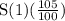 =
=
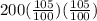 =
=
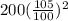
.
.
.
.
.
Similarly
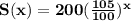
The predicted amount spent per student over time, A(t)
Rate of decrements is 2% per year.
A function 'A(t)' which gives the amount spend on each student in school after 't' years.
A(0) means the initial year when the number of students is 40.
A(0) = 40
A(1) means the amount spend on each student in school after one year when the amount decreased by 2% than previous year which is 40.
A(1) = 40 + 2% of 40 =
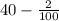 =
=
 =
=
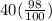
A(2) means the amount spend on each student in school after two year when the amount decreased by 2% than previous year which is A(1)
A(2) = A(1) + 2% of A(1) =
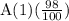 =
=
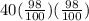 =
=

.
.
.
.
.
Similarly
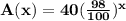
The predicted total expense for supplies each year over time, E(t)
Total expense = (number of students) × (amount spend on each student)
E(t) = S(t) × A(t)
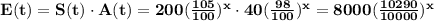
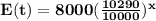
(NOTE : The value of x in all the above equation is between zero(0) to ten(10).)