The given system of equations has only one solution
The solution is (x, y) = (-1, 0)
Solution:
Given system of equations are:
-7x - 2y = 7 ---- eqn 1
4x + 6y = -4 --- eqn 2
We have to find solution for this system of equations by substitution method
From eqn 2,
4x + 6y = -4
2x + 3y = -2
2x = -2 - 3y
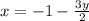 --- eqn 3
--- eqn 3
Substitute eqn 3 in eqn 1
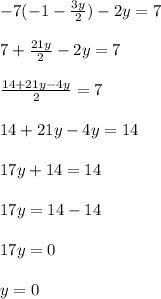
y = 0
Substitute y = 0 in eqn 1
-7x -2(0) = 7
-7x = 7
x = -1
Thus the solution is (x, y) = (-1, 0)
Therefore the given system of equations has only one solution