Question

Which equation has the components of 0 = x2 – 9x – 20 inserted into the quadratic formula correctly? x = StartFraction negative 9 plus or minus StartRoot (negative 9) squared minus 4(1)(negative 20) EndRoot Over 2(1) EndFraction x = StartFraction 9 plus or minus StartRoot (negative 9) squared minus 4(1)(20) EndRoot Over 2(1) EndFraction x = StartFraction 9 plus or minus StartRoot (negative 9) squared minus 4(1)(negative 20) EndRoot Over 2(1) EndFraction x = StartFraction negative 9 plus or minus StartRoot (negative 9) squared + 4(1)(negative 20) EndRoot Over 2(1) EndFraction

Answer 1

Answer: C

Step-by-step explanation: No cap

Answer 2

`x=(9+/-√((-9)^2-4\,(1)\,(-20)) )/(2\,(1))`

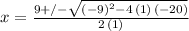
Explanation:

Recall that the quadratic formula gives you the pattern to follow in order to find the solutions to a quadratic equation of the form:
`ax^2+bx+c=0`

It tells us that we need to use the parameters
`a,\, b,` and
`c` in the following formula in order to get the answers for the x-values that solve it:

`x=(-b+/-√(b^2-4\,a\,c) )/(2\,a)`

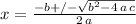
so, in our case,
`a=1`,
`b=-9`, and
`c=-20`

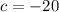
then, replacing these values in the formula, we obtain:

`x=(-b+/-√(b^2-4\,a\,c) )/(2\,a)\\x=(-(-9)+/-√((-9)^2-4\,(1)\,(-20)) )/(2\,(1))\\x=(9+/-√((-9)^2-4\,(1)\,(-20)) )/(2\,(1))`

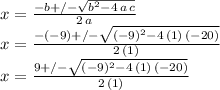
Which looks like the third expression you are listing (although it is a little hard to read)