Answer:
x=30° or 210°
Explanation:
The given equation is:

Taking the second term to RHS we get
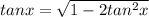
Squaring both sides of the equation,we get
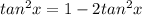
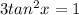
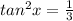
∴tanx=±
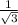
But tanx cannot be negative as RHS in the given equation will be positive always. Hence tanx=
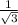
∴ x=30° or x=180°+30°=210° (As tan is positive in first and third quadrant)