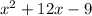Question

Solve this problem out

Answer 1

Option C

When
`(2x - 3)^2` is subtracted from
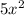`5x^2` then the result is
`x^2 + 12x - 9`

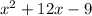
Solution:

Given that
`(2x - 3)^2` is subtracted from
`5x^2`

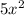
We have to find the result

Subtraction is a mathematical operation that tells us the difference between two numbers.

When "a" is subtracted from "b", we write in mathematical expression as "b - a"

So
`(2x - 3)^2` is subtracted from
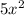`5x^2` is written mathematically as:

`\rightarrow 5x^2 - (2x - 3)^2`

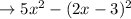
Expanding the above expression using algebraic identity:

`(a-b)^2 = a^2 - 2ab + b^2`

`\rightarrow 5x^2 - ((2x)^2 -2(2x)(3) + (3)^2)\\\\\rightarrow 5x^2 - (4x^2 - 12x + 9)`

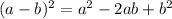
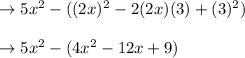
Multiplying the nnegative sign with terms inside bracket

There are two simple rules to remember:

• When you multiply a negative number by a positive number then the product is always negative.

• When you multiply two negative numbers or two positive numbers then the product is always positive.

`\rightarrow 5x^2 - (4x^2 - 12x + 9)\\\\\rightarrow 5x^2 - 4x^2 + 12x -9\\\\\rightarrow x^2 + 12x - 9`

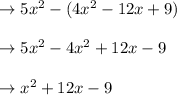
Hence the result is:
`x^2 + 12x - 9`