Question

Find the consecutive positive odd integers whose product is 99​

Answer 1

9 and 11

Explanation:

So let's say that the first integer is x.

That means that the second integer is x+2, since it us the next odd number.

This problem can be easily solved with our mind the answer is 9 and 11, but I'll show you the steps to slove this.

We make an equation using these two numbers:

`(x)*(x+2)=99\\`

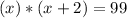
Now all we gotta do is solve for x:

`x^2 +2x = 99\\x^2+2x-99=0`

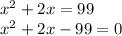
Now we use either splitting the middle term or quadratic formula:

`x^2+11x-9x+99=0\\x(x+11)-9(x+11)=0\\(x+11)(x-9)=0`

Now we split each terma and solve for x:

`(x-9)=0\\x=9\\(x+11)=0\\x=-11`

Now the question states positive so we can rule out x = -11.

Now we have the first integer x = 9,

the second integer is x+2 = 9+2 =11

So the two consecutive positive odd integers are 9 and 11