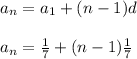Question

Write an equation for the nth term of the arithmetic sequence. Then find a₁₀.


`(1)/(7), (2)/(7), (3)/(7), (4)/(7) , . . .`

Answer 1

The equation for nth term of the arithmetic sequence:
`a_n = (1)/(7) + (n - 1)(1)/(7)`

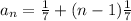
The value of
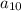`a_(10)` is
`(10)/(7)`

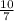
Solution:

Given that arithmetic sequence is:

`(1)/(7) , (2)/(7) , (3)/(7) , (4)/(7) , .......`

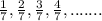
To find: Equation for the nth term of the arithmetic sequence and
`a_(10)`

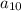
The formula for finding nth term in arithmetic sequence is given as:

`a_(n)=a_(1)+(n-1)d`

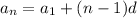
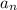`a_n` = the nᵗʰ term in the sequence

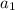`a_1` = the first term in the sequence

d = the common difference between consecutive terms

common difference between consecutive terms =
`(2)/(7) - (1)/(7) = (1)/(7)`

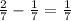
Here first term
`a_1 = (1)/(7)`

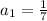
Finding
`a_(10)`

`a_(10) = (1)/(7) + (10 - 1) (1)/(7)\\\\a_(10) = (1)/(7) + 9 * (1)/(7)\\\\a_(10) = (1)/(7) + (9)/(7)\\\\a_(10) = (10)/(7)`

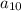
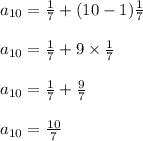
Thus the equation for nth term of the arithmetic sequence:

`a_(n)=a_(1)+(n-1)d\\\\a_n = (1)/(7) + (n - 1)(1)/(7)`