Answer:
Check the two conditions of Subspace.
Explanation:
If W is a Subspace of a vector space, V then it should satisft the following conditions.
1) The zero element should be in W.
Zero element can be different for different vector spaces. For examples, zero vector in
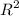 is (0, 0) whereas, zero element in
is (0, 0) whereas, zero element in
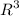 is (0, 0 ,0).
is (0, 0 ,0).
2) For any two vectors,
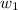 and
and
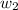 in W,
in W,
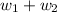 should also be in W.
should also be in W.
That is, it should be closed under addition.
3) For any vector
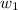 in W and for any scalar,
in W and for any scalar,
 in V,
in V,
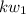 should be in W.
should be in W.
That is it should be closed in scalar multiplication.
The conditions are mathematically represented as follows:
1) 0
 W.
W.
2) If
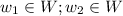 then
then
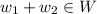 .
.
3)
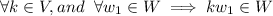
Here V =
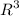 and W = Set of all (x, y, z) such that
and W = Set of all (x, y, z) such that
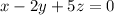
We check for the conditions one by one.
1) The zero vector belongs to the subspace, W. Because (0, 0, 0) satisfies the given equation.
i.e., 0 - 2(0) + 5(0) = 0
2) Let us assume
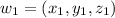 and
and
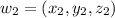 are in W.
are in W.
That means:
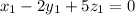 and
and

We should check if the vectors are closed under addition.
Adding the two vectors we get:
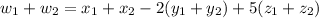
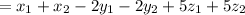
Rearranging these terms we get:
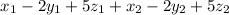
So, the equation becomes, 0 + 0 = 0
So, it s closed under addition.
3) Let k be any scalar in V. And
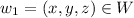
This means
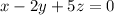

Taking k common outside, we get:
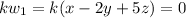
The equation becomes k(0) = 0.
So, it is closed under scalar multiplication.
Hence, W is a subspace of
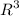 .
.