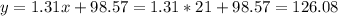Question

Modern medical practice tells us not to encourage babies to become too fat. Is there a positive correlation between the weight x of a 1-year old baby and the weight y of the mature adult (30 years old)? A random sample of medical files produced the following information for 14 females. x (lb) 23 23 21 26 20 15 25 21 17 24 26 22 18 19 y (lb) 127 122 119 125 130 120 145 130 130 130 130 140 110 115 In this setting we have Σx = 300, Σy = 1773, Σx2 = 6576, Σy2 = 225,649, and Σxy = 38,186.

Answer 1

a) Figure attached

b)
`y=1.31 x +98.57`

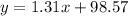
c) The correlation coefficient would be r =0.47719

d)
`y=1.31 x +98.57=1.31*21 + 98.57 =126.08`

Explanation:

(a) Draw a scatter diagram for the data.

See the figure attached

(b) Find x, y, b, and the equation of the least-squares line. (Round your answers to three decimal places.) x =__ y =__ b =__ y =__ + __x

`m=(S_(xy))/(S_(xx))`

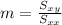
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

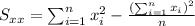
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=6576-(300^2)/(14)=147.429`

`S_(xy)=\sum_(i=1)^n x_i y_i -\frac{(\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i){n}}=38186-(300*1773)/(14)=193.143`

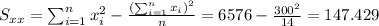
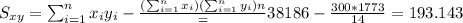
And the slope would be:

`m=(193.143)/(147.429)=1.31`

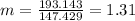
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(300)/(14)=21.429`

`\bar y= (\sum y_i)/(n)=(1773)/(14)=126.643`

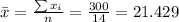
And we can find the intercept using this:

`b=\bar y -m \bar x=126.643-(1.31*21.429)=98.571`

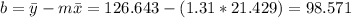
So the line would be given by:

`y=1.31 x +98.57`

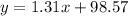
(c) Find the sample correlation coefficient r and the coefficient of determination r?2. (Round your answers to three decimal places.)

n=14
`\sum x = 300, \sum y = 1773, \sum xy=38186, \sum x^2 =6576, \sum y^2 =225649`

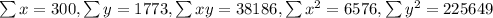
And in order to calculate the correlation coefficient we can use this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

`r=(14(38186)-(300)(1773))/(√([14(6576) -(300)^2][14(225649) -(1773)^2]))=0.9534`

So then the correlation coefficient would be r =0.47719

What percentage of variation in y is explained by the least-squares model? (Round your answer to one decimal place.)

The % of variation is given by the determination coefficient given by
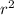`r^2` and on this case
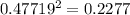`0.47719^2 =0.2277`, so then the % of variation explaines is 22.8%.

(d) If a female baby weighs 21 pounds at 1 year, what do you predict she will weigh at 30 years of age? (Round your answer to two decimal places.) ___ lb

So we can replace in the linear model like this:

`y=1.31 x +98.57=1.31*21 + 98.57 =126.08`